基爾霍夫（電路）定律(Kirchhoff laws)是電路中電壓和電流所遵循的基本規律，是分析和計算較為(wei) 複雜電路的基礎，1845年由德國物理學家G.R.基爾霍夫（Gustav Robert Kirchhoff，1824～1887）提出。基爾霍夫（電路）定律包括基爾霍夫電流定律（KCL）和基爾霍夫電壓定律（KVL）。
基爾霍夫（電路）定律既可以用於(yu) 直流電路的分析，也可以用於(yu) 交流電路的分析，還可以用於(yu) 含有電子元件的非線性電路的分析。

中文名：基爾霍夫定律
外文名：Kirchhoff's law
別    稱 KCL   KVL
提出者：G.R.基爾霍夫
提出時間：1845年
應用學科：電路基礎

發現背景
基爾霍夫定律是求解複雜電路的電學基本定律。從(cong) 19世紀40年代，由於(yu) 電氣技術發展的十分迅速，電路變得愈來愈複雜。某些電路呈現出網絡形狀，並且網絡中還存在一些由3條或3條以上支路形成的交點(節點)。這種複雜電路不是串、並聯電路的公式所能解決(jue) 的。
剛從(cong) 德國哥尼斯堡大學畢業(ye) ，年僅(jin) 21歲的基爾霍夫在他的第1篇論文中提出了適用於(yu) 這種網絡狀電路計算的兩(liang) 個(ge) 定律，即著名的基爾霍夫定律。該定律能夠迅速地求解任何複雜電路，從(cong) 而成功地解決(jue) 了這個(ge) 阻礙電氣技術發展的難題。
由於(yu) 似穩電流(低頻交流電)具有的電磁波長遠大於(yu) 電路的尺度，所以它在電路中每一瞬間的電流與(yu) 電壓均能在足夠好的程度上滿足基爾霍夫定律。因此，基爾霍夫定律的應用範圍亦可擴展到交流電路之中。

基本概念
1、支路：
（1）每個(ge) 元件就是一條支路。
（2）串聯的元件我們(men) 視它為(wei) 一條支路。
（3）在一條支路中電流處處相等。 [2]
2、節點：
（1）支路與(yu) 支路的連接點。
（2）兩(liang) 條以上的支路的連接點。
（3）廣義(yi) 節點（任意閉合麵）。
3、回路：
（1）閉合的支路。
（2）閉合節點的集合。
4、網孔：
（1）其內(nei) 部不包含任何支路的回路。
（2）網孔一定是回路，但回路不一定是網孔。

基爾霍夫第一定律（KCL）定義(yi)
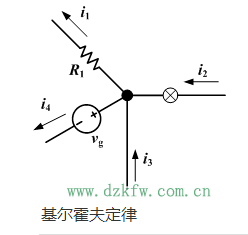
基爾霍夫第一定律又稱基爾霍夫電流定律，簡記為(wei) KCL，是電流的連續性在集總參數電路上的體(ti) 現，其物理背景是電荷守恒公理。基爾霍夫電流定律是確定電路中任意節點處各支路電流之間關(guan) 係的定律，因此又稱為(wei) 節點電流定律。基爾霍夫電流定律表明：
所有進入某節點的電流的總和等於(yu) 所有離開這節點的電流的總和。
或者描述為(wei) ：
假設進入某節點的電流為(wei) 正值，離開這節點的電流為(wei) 負值，則所有涉及這節點的電流的代數和等於(yu) 零。
以方程表達，對於(yu) 電路的任意節點滿足：

其中，  是第k個(ge) 進入或離開這節點的電流，是流過與(yu) 這節點相連接的第k個(ge) 支路的電流，可以是實數或複數。
應用方法
在列寫(xie) 節點電流方程時，各電流變量前的正、負號取決(jue) 於(yu) 各電流的參考方向對該節點的關(guan) 係（是“流入”還是“流出”）；而各電流值的正、負則反映了該電流的實際方向與(yu) 參考方向的關(guan) 係（是相同還是相反）。
通常規定，對參考方向背離（流出）節點的電流取正號，而對參考方向指向（流入）節點的電流取負號。

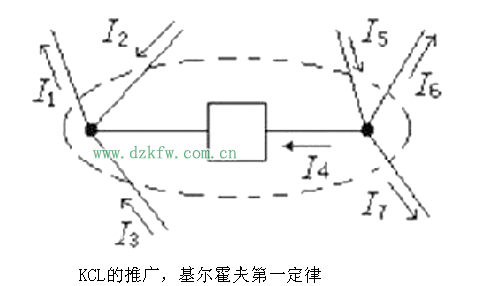
KCL定律不僅(jin) 適用於(yu) 電路中的節點，還可以推廣應用於(yu) 電路中的任一不包含電源的假設的封閉麵。即在任一瞬間，通過電路中任一不包含電源的假設封閉麵的電流代數和為(wei) 零。
圖KCL的推廣所示為(wei) 某電路中的一部分，選擇封閉麵如圖中虛線所示，在所選定的參考方向下有：

推導
由於(yu) 累積的電荷（單位為(wei) 庫侖(lun) ）是電流（單位為(wei) 安培）與(yu) 時間（單位為(wei) 秒）的乘積，從(cong) 電荷守恒定律可以推導出這條定律。其實質是穩恒電流的連續性方程，即根據電荷守恒定律，流向節點的電流之和等於(yu) 流出節點的電流之和。
思考電路的某節點，跟這節點相連接有個(ge) 支路。假設進入這節點的電流為(wei) 正值，離開這節點的電流為(wei) 負值，則經過這節點的總電流等於(yu) 流過支路的電流的代數和：

將這方程積分於(yu) 時間，可以得到累積於(yu) 這節點的電荷的方程：

其中，   是累積於(yu) 這節點的總電荷，  是流過支路 k 的電荷，t 是檢驗時間， t'是積分時間變量。
假設，q>0則正電荷會(hui) 累積於(yu) 節點；否則，負電荷會(hui) 累積於(yu) 節點。根據電荷守恒定律， q 是個(ge) 常數，不能夠隨著時間演進而改變。由於(yu) 這節點是個(ge) 導體(ti) ，不能儲(chu) 存任何電荷。所以，q=0 、i=0 ，基爾霍夫電流定律成立：

基爾霍夫第二定律（KVL）定義(yi)
基爾霍夫第二定律又稱基爾霍夫電壓定律，簡記為(wei) KVL，是電場為(wei) 位場時電位的單值性在集總參數電路上的體(ti) 現，其物理背景是能量守恒。基爾霍夫電壓定律是確定電路中任意回路內(nei) 各電壓之間關(guan) 係的定律，因此又稱為(wei) 回路電壓定律。
基爾霍夫電壓定律表明：
沿著閉合回路所有元件兩(liang) 端的電勢差（電壓）的代數和等於(yu) 零。
或者描述為(wei) ：
沿著閉合回路的所有電動勢的代數和等於(yu) 所有電壓降的代數和。
以方程表達，對於(yu) 電路的任意閉合回路，

其中，m 是這閉合回路的元件數目， vk是元件兩(liang) 端的電壓，可以是實數或複數。
基爾霍夫電壓定律不僅(jin) 應用於(yu) 閉合回路，也可以把它推廣應用於(yu) 回路的部分電路。

應用方法
KVL定律是描述電路中組成任一回路上各支路（或各元件）電壓之間的約束關(guan) 係，沿選定的回路方向繞行所經過的電路電位的升高之和等於(yu) 電路電位的下降之和。
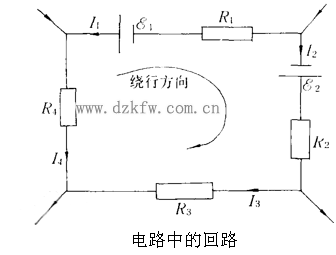
應用該方程時，應先在回路中選定一個(ge) 繞行方向作為(wei) 參考，則電動勢與(yu) 電流的正負號就可規定如下： 電動勢的方向 (由負極指向正極)與(yu) 繞行方向一致時取正號，反之取負號; 同樣，電流的方向與(yu) 繞行方向一致時取正號，反之取負號。例如，用此規定可將回路(如圖2)的基爾霍夫電壓方程寫(xie) 成：

-E1+E2=-I1R1+I2R2+I3R3-I4R4

每個(ge) 閉合回路均可列出一個(ge) 方程。如果某回路至少有一個(ge) 支路未被其他方程用過，則稱此回路為(wei) 獨立回路。對於(yu) 存在M個(ge) 獨立回路的電路，可以列出M個(ge) 獨立的回路電壓方程，它們(men) 組成的方程組稱為(wei) 基爾霍夫第二方程組。

適用範圍
基爾霍夫定律建立在電荷守恒定律、歐姆定律及電壓環路定理的基礎之上，在穩恒電流條件下嚴(yan) 格成立。當基爾霍夫第一、第二方程組聯合使用時，可正確迅速地計算出電路中各支路的電流值。由於(yu) 似穩電流(低頻交流電) 具有的電磁波長遠大於(yu) 電路的尺度，所以它在電路中每一瞬間的電流與(yu) 電壓均能在足夠好的程度上滿足基爾霍夫定律。因此，基爾霍夫定律的應用範圍亦可擴展到交流電路之中。
它除了可以用於(yu) 直流電路的分析，和用於(yu) 似穩電路的分析，還可以用於(yu) 含有電子元件的非線性電路的分析。運用基爾霍夫定律進行電路分析時，僅(jin) 與(yu) 電路的連接方式有關(guan) ，而與(yu) 構成該電路的元器件具有什麽(me) 樣的性質無關(guan) 。
但用於(yu) 交流電路的分析是，即對通過含時電流的電路進行分析時，由於(yu) 通過閉合回路的磁通量是時間的函數，根據法拉第電磁感應定律，會(hui) 有電動勢E出現於(yu) 閉合回路。所以，電場沿著閉合回路的線積分不等於(yu) 零。此時回路方程應寫(xie) 作：
Σvk = E = - ΔΦ/Δt (磁場正方向與(yu) 回路正方向相同時)
這是因為(wei) 電流會(hui) 將能量傳(chuan) 遞給磁場；反之亦然，磁場亦會(hui) 將能量傳(chuan) 遞給電流。
對於(yu) 含有電感器的電路，必需將基爾霍夫電壓定律加以修正。由於(yu) 含時電流的作用，電路的每一個(ge) 電感器都會(hui) 產(chan) 生對應的電動勢Ek。必需將這電動勢納入基爾霍夫電壓定律，才能求得正確答案。