1、戴維南定理

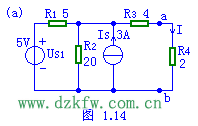
　　圖1.14(a)中,電路結構和參數已給定,應用戴維南定理求電流I=？(圖中電阻的單位為(wei) 歐姆)。

　　分析：應用戴維南定理的關(guan) 鍵是求出a,b兩(liang) 端的開路電壓Uoc和入端電阻Req。Uoc等於(yu) ab兩(liang) 端將負載開路後的電壓；Req等於(yu) 將ab左邊的含源二端網絡變為(wei) 無源二端網絡時的入端電阻。 求開路電壓的等效電路如圖(b)所示,方法不限。本題用結點電壓法。入端電阻的等效電路如(c)所示；利用圖(d)求出待求量。

　方程式及結果如下：
　將負載開路,如(b)。在(b)中求ab兩(liang) 端的開路電壓Uoc：
　[(1/R1)+(1/R2)]Uoc=(Us1/R1)+IS 代入數據, 解得 Uoc=32V
　為(wei) 求入端電阻，在(b)中，將獨立源置零，如(c)。則ab兩(liang) 端的入端電阻： Req=4+5//20=8Ω
　則戴維南等效電路如圖(d)。電流 I=32/(8+2)=3.2A  

2、諾頓定理

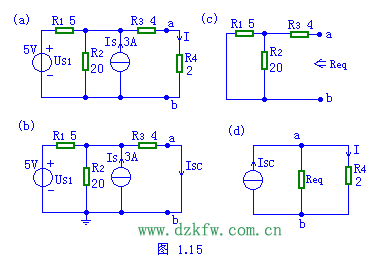
　　圖1.15(a)中,電路結構和參數已給定,用諾頓定理求電流I=？(圖中電阻的單位為(wei) 歐姆)。

　　分析：應用諾頓定理的關(guan) 鍵是求出a,b兩(liang) 端的短路電流Isc和入端電阻Req(或電導Geq),Isc等於(yu) ab兩(liang) 端將負載短路時的電流如圖(b)所示；Req(或電導Geq)等於(yu) 將ab左邊的含源二端網絡變為(wei) 無源二端網絡時的入端電阻(或電導), 其等效電路如 (c)所示；最後利用圖(d)求得待求量。

　方程式及結果如下：

3、含有受控源的戴維南定理

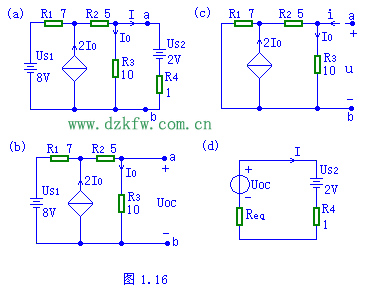
　　圖1.16(a)中,電路結構和參數已給定,求：電流I=？(電阻的單位為(wei) 歐姆)。

　　分析：該電路中含有CCCS,為(wei) 了求開路電壓Uoc，仍須將ab支路斷開如圖(b)所示，用任意方法求開路電壓，根據電路特點用結點電壓法。當電路中有受控源時求入端電阻的方法與(yu) 無受控源時不太一樣。有兩(liang) 種方法可采用，一是除獨立源後，加壓求電流，入端電阻Req=u/i,如(c)所示，可用任意方法求出u/i，本題采用基爾霍夫定律。最後利用圖(d)求出待求量。

　方程式及結果如下：

4、戴維南定理綜合題目

　　分析：該電路中含有CCCS，解題思路與(yu) 上一題類似，為(wei) 了求開路電壓Uoc仍須將ab支路斷開如圖(b)所示，用任意方法求開路電壓。本題用網孔電流法，網孔電流如(b)紅線所示。在含有受控源的電路中，求入端電阻除了采用除獨立源加壓求電流外，還可以用開路電壓除以短路電流，即Req=Uoc/ISC求入端電阻。首先將負載短路，如(c)，其中短路電流ISC，可用任意方法求短路電流ISC。最後得到戴維南等效電路(d)，即可求I。

　方程式及結果如下：

5、最大功率傳(chuan) 輸定理

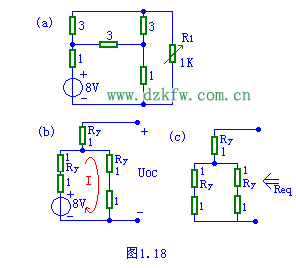
　　圖1.18(a)電路中,求R為(wei) 何值時，負載 R 可獲得最大功率，並求出Pmax。(圖中未標電阻的單位為(wei) 歐姆)。

　　分析：根據最大功率的傳(chuan) 輸定理，當負載電阻等於(yu) 電壓源的內(nei) 阻時，負載可獲得最大有功功率。因此本題的關(guan) 鍵是求出該電路的戴維南等效電路。即Uoc如圖(b)和Req如圖(c)所示。具體(ti) 計算過程和以上題目類似，計算過程中用到電阻的三角形與(yu) 星形之間的轉換。

　方程式及結果如下：

　首先將三個(ge) ３Ω電阻等效轉換成Ｙ型連接RY＝１Ω， 網孔電流 I=8/4=2A
　則：Uoc=2I=4V
　在(c)中求ab兩(liang) 端的入端電阻：Req=1+2//2=2歐,
　因此根據最大功率傳(chuan) 輸定理：當R=2Ω時R可獲得最大有功功率

　Pmax=( Uoc*Uoc)/4*Req=2w