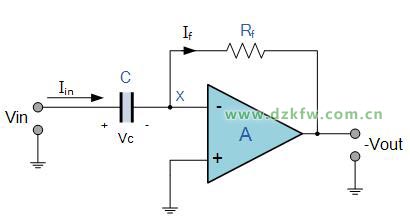
微分放大器,顧名思義(yi) ,就是在運算電路中執行微分運算的電路。與(yu) 反向放大器類似,我們(men) 調換一下電容器和電阻器的位置,既將電抗X C連接到反相放大器的輸入端子,而電阻器Rf像往常一樣在運算放大器上形成負反饋元件。如下圖:
該運算放大器電路執行微分的數學運算,即“產(chan) 生的輸出電壓與(yu) 輸入電壓相對於(yu) 時間的變化率成正比”。換句話說,輸入電壓信號的變化越快或越大,輸入電流越大,響應時輸出電壓的變化就越大,形狀越像“尖峰”。
與(yu) 積分器電路一樣,將一個(ge) 電阻器和一個(ge) 電容器構成一個(ge) 跨運算放大器的RC網絡,而電容器的電抗(Xc)在運算放大器微分器的性能中起著重要作用。
運算放大器微分電路介紹
差分器的輸入信號被施加到電容器。電容器阻止任何直流成分,因此沒有電流流向放大器的求和點X,導致輸出電壓為(wei) 零。該電容器僅(jin) 允許交流型輸入電壓的變化通過,其頻率取決(jue) 於(yu) 輸入信號的變化率。
在低頻下,電容器的電抗為(wei) “高”,從(cong) 而導致低增益(Rf/ Xc)和運算放大器的低輸出電壓。在較高的頻率下,電容器的電抗要低得多,從(cong) 而導致差分放大器的增益更高,輸出電壓更高。
然而,在高頻下,運算放大器的微分電路變得不穩定,並且將開始振蕩。這主要歸因於(yu) 一階效應,它決(jue) 定了運算放大器電路的頻率響應,從(cong) 而引起二階響應,在高頻下,二階響應給出的輸出電壓遠高於(yu) 預期。為(wei) 避免這種情況,需要通過在反饋電阻Rf兩(liang) 端增加一個(ge) 額外的小電容來降低電路的高頻增益。
由於(yu) 運算放大器在其反相輸入端的節點電壓為(wei) 零,因此流過電容器的電流I將給出為(wei) :
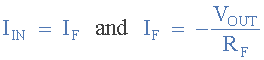
電容器上的電荷等於(yu) 電容乘以電容器兩(liang) 端的電壓:
![]()
因此,此費用的變化率是:
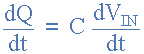
但DQ / dt是電容器電流,I:
從(cong) 中我們(men) 可以得出運算放大器微分器的理想電壓輸出為(wei) :
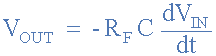
因此,輸出電壓Vout為(wei) 常數–Rf*C乘以輸入電壓Vin相對於(yu) 時間的導數。負號(–)表示相移180°,因為(wei) 輸入信號連接到運算放大器的反相輸入端子。
最後要提到的一點是,與(yu) 以前的運算放大器積分器電路相比,基本形式的運算放大器微分器電路有兩(liang) 個(ge) 主要缺點。一個(ge) 是如上所述的,它在高頻下會(hui) 遭受不穩定的影響,另一個(ge) 是,電容性輸入使其非常容易受到隨機噪聲信號的影響,並且源電路中存在的任何噪聲或諧波都將比輸入信號本身被放大更多。這是因為(wei) 輸出與(yu) 輸入電壓的斜率成正比,因此需要一些限製帶寬的方法以實現閉環穩定性。
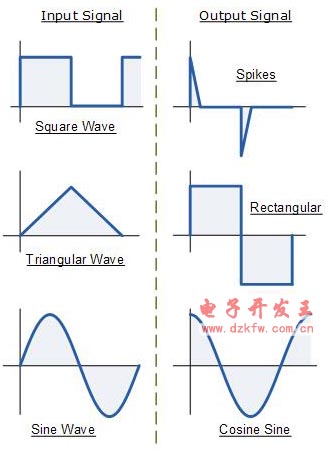
運算放大器微分器波形
如果我們(men) 將持續變化的信號(例如方波,三角或正弦波類型的信號)施加到微分放大器電路的輸入,則最終的輸出信號將發生變化,其最終形狀取決(jue) 於(yu) 電阻的RC時間常數/電容器組合。
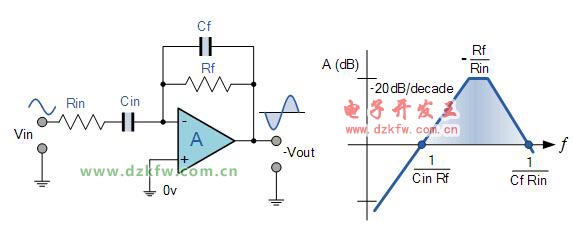
基本的單電阻器和單電容器運算放大器微分器電路由於(yu) 上述兩(liang) 個(ge) 固有的錯誤(“不穩定”和“噪聲”)而沒有廣泛用於(yu) 改革微分的數學函數。因此,為(wei) 了降低電路在高頻下的整體(ti) 閉環增益,需要在輸入端添加一個(ge) 額外的電阻Rin,如下所示。
添加輸入電阻器R IN限製了微分器以Rf/ R IN的比率增加的增益。該電路現在在低頻下就像一個(ge) 微分器放大器,而在高頻下像一個(ge) 具有電阻反饋的放大器,可以提供更好的噪聲抑製。
通過將電容器Cf與(yu) 微分器反饋電阻Rf並聯連接,可以實現更高頻率的附加衰減。這樣就構成了有源高通濾波器的基礎,正如我們(men) 之前在濾波器部分所看到的那樣。


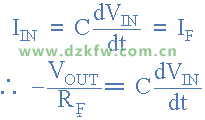
 返回頂部
返回頂部 刷新頁麵
刷新頁麵 下到頁底
下到頁底