在數字電路中，卡諾圖是用最小項方格表示邏輯函數的方法，其是用圖形表示輸入變量與(yu) 函數之間的邏輯關(guan) 係，它用幾何位置上的相鄰，形象地表示了組成邏輯函數的各個(ge) 最小項之間在邏輯上的相鄰性。初學者往往以為(wei) 卡諾圖隻是數字電路分析和設計中用以化簡邏輯函數的一種工具。其實不然，實際上靈活運用卡諾圖，可以使邏輯電路的分析和設計過程大大地簡化，讓一些難題迎刃而解。下麵介紹卡諾圖在化簡之外的幾點靈活運用。

　　1 卡諾圖的應用

　　1.1 利用卡諾圖結構幫助記憶格雷碼

　　格雷碼是一種常用的無權BCD碼，相鄰兩(liang) 碼之間隻有一位二進製數碼不同。常用於(yu) 模擬量的轉換中，當模擬量發生微小變化而可能引起數字量發生變化時，格雷碼僅(jin) 改變1位，這樣與(yu) 其他碼同時改變兩(liang) 位或多位的情況相比更為(wei) 可靠，可減少出錯的可能性，提高電路的抗幹擾能力，它是一種典型的可靠性代碼，這種碼製在數控裝置中有著廣泛的應用。但由於(yu) 這種編碼所具有的獨特性，實際應用中很難記憶。經研究和探討，我們(men) 觀察到利用卡諾圖按照一定規律取值，可用於(yu) 實現記憶格雷碼。這種獨特的記憶方式，可幫助學生方便、輕鬆地記住該編碼，並應用於(yu) 實際中。

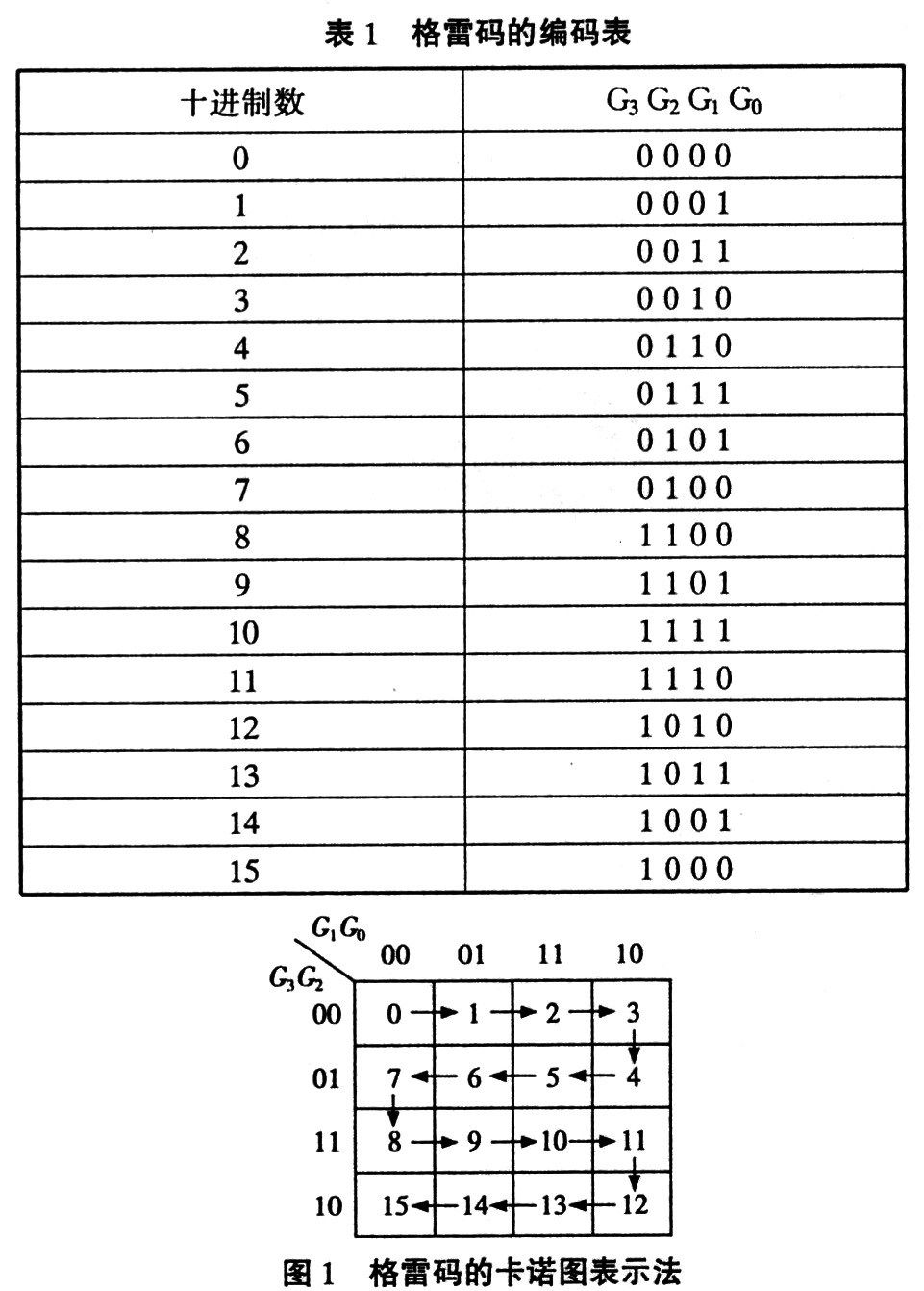
　　選用四變量卡諾圖並令：G3G2G1G0分別作為(wei) 四位格雷碼的輸入變量。將變量G3G2作為(wei) 高位，GlGO作為(wei) 低位。畫出四變量卡諾圖。從(cong) 四變量卡諾圖中我們(men) 可見，卡諾圖中四變量若按箭頭所示的方向順序取值，其所取的值變化順序正好即為(wei) 四位格雷碼的編碼表，如圖1格雷碼的卡諾圖表示法所示。十進製數從(cong) 0～15，對應四位格雷碼的輸入代碼依次分別為(wei) 0000—0001—0011——1001一1000，如表l所示格雷嗎碼的編碼表。

　　1.2 卡諾圖在組合邏輯電路競爭(zheng) 冒險中的應用

　　競爭(zheng) 冒險，是數字電路中一種特有的現象。不同的門電路有著不同的延遲時間，輸入信號經過不同的途徑進行傳(chuan) 輸，到達輸出端的時間有早有遲，狀態變化有先有後，存在時差。這種狀態變化存在時差的現象就叫做“競爭(zheng) ”。如果競爭(zheng) 結果是使穩態輸出的邏輯關(guan) 係受到短暫破壞，出現不應有的尖峰脈衝(chong) ，這種現象就叫做“冒險”。冒險可能使電路產(chan) 生暫時或永久的邏輯錯誤。

　　在進行邏輯電路設計時，我們(men) 必須應發現和判別出產(chan) 生競爭(zheng) 冒險的可能，並采取積極有效的措施將競爭(zheng) 冒險予以消除。判斷和消除競爭(zheng) 冒險的方法很多，最簡便和最直觀的方法就是使用卡諾圖。

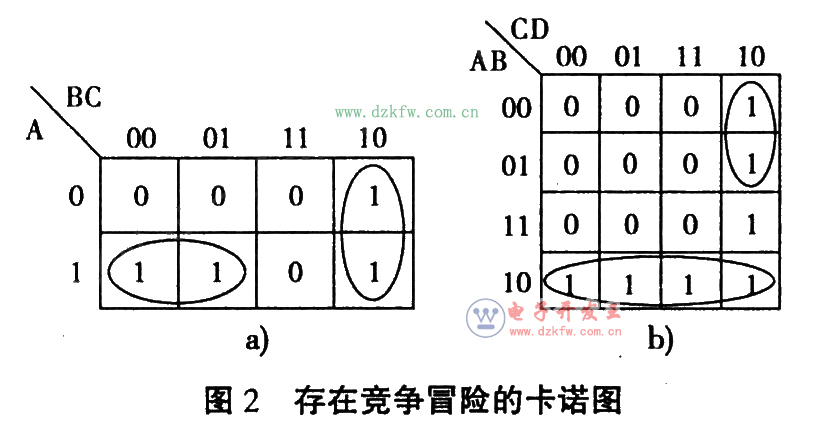
　　使用卡諾圖判斷一個(ge) 組合邏輯電路是否存在著競爭(zheng) 冒險的一般步驟是：首先畫出該電路邏輯函數的卡諾圖，然後在函數卡諾圖上畫出與(yu) 表達式中所有乘積項相對應的卡諾圈，如果圖中有相切的卡諾圈，則該邏輯電路存在著競爭(zheng) 冒險如圖2所示，所謂卡諾圈相切即兩(liang) 個(ge) 卡諾圈之間存在不被同一卡諾圈包含的相鄰最小項。

　　如果邏輯函數的卡諾圖中存在著相切的卡諾圈，該邏輯電路就存在著競爭(zheng) 冒險;那麽(me) ，隻要使函數的卡諾圖中消除相切的卡諾圈，即可消除競爭(zheng) 冒險現象。在卡諾圖上，加上一個(ge) 與(yu) 兩(liang) 相切卡諾圈相交的一個(ge) 圈(一項)，破壞卡諾圈的單獨相切性。加上此圈後，邏輯函數多了一個(ge) 冗餘(yu) 項，冗餘(yu) 項的加入並不改變原邏輯函數的邏輯值，但冗餘(yu) 項的加入卻可以有效地消除冒險。

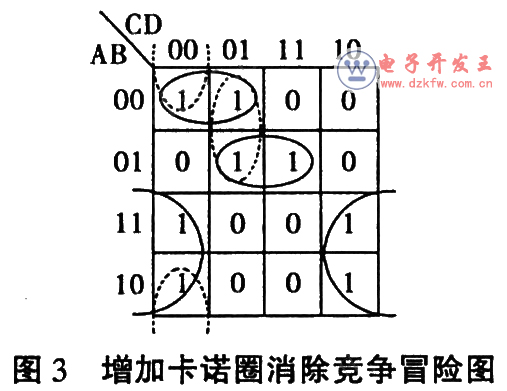
　　例如圖3所示的卡諾圖中，有兩(liang) 處存在卡諾圈相切現象，故其表示的邏輯函數式F=ABC十ABD+AD存在冒險。可加兩(liang) 個(ge) 卡諾圈(虛線圈)破壞其相切性，也即增加兩(liang) 個(ge) 冗餘(yu) 項BCD和ACD，消除競爭(zheng) 冒險後，該邏輯函數的表達式如下所示：

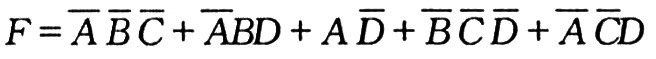
　　由此可見，使用卡諾圖判斷和消除數字電路中的競爭(zheng) 冒險，簡便直觀，易於(yu) 操作。

　　1.3 用卡諾圖完成兩(liang) 邏輯函數的邏輯運算

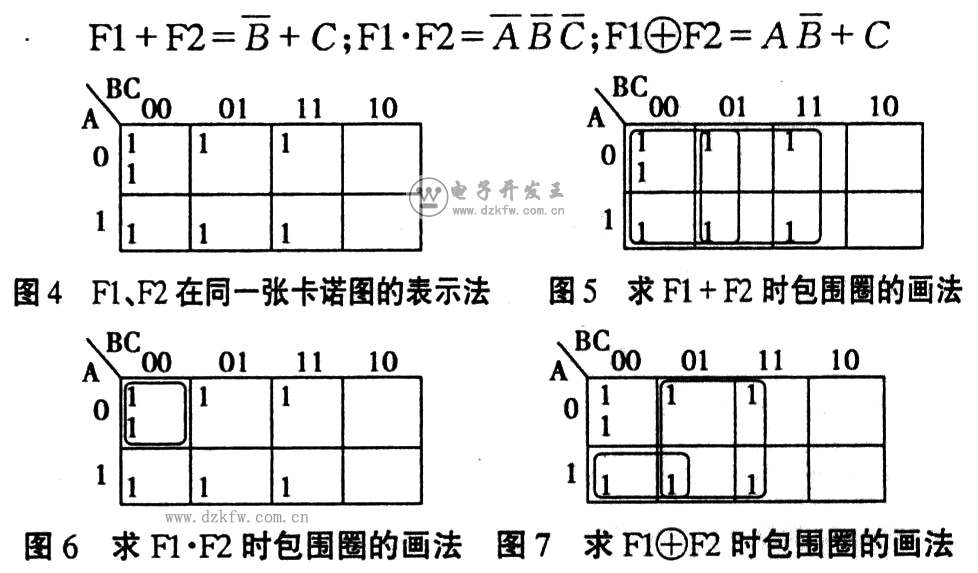
　　首先將邏輯函數F1和F2在同一張卡諾圖中表示出來。為(wei) 區別起見，將函數F1出現的l填在卡諾圖小方格的左上角，將另一函數F2出現的l填在卡諾圖小方格的左下角。

　　下麵以幾個(ge) 常見的邏輯運算為(wei) 例來說明。

　　1)求兩(liang) 邏輯函數Y1和Y2的或運算F1+F2

　　根據或運算的特點，求或運算時，隻要將Y1、Y2卡諾圖中出現的所有l都畫入包圍圈，然後根據卡諾圖寫(xie) 出表達式。

　　2)求兩(liang) 邏輯函數Fl和F2的與(yu) 運算Fl·F2

　　根據與(yu) 運算的特點，求與(yu) 運算時，隻要將F1、F2卡諾圖中重複出現的l畫入包圍圈，然後根據卡諾圖寫(xie) 出表達式。

　　3)求兩(liang) 邏輯函數Fl和F2的異或運算Fl+F2

　　根據異或運算的特點，求異或運算時，隻要將Fl、F2卡諾圖中不重複出現的l畫入包圍，然後根據卡諾圖寫(xie) 出表達式。

　　例：已知兩(liang) 邏輯函數F1(A，B，C)=∑m(0，1，3)，F2(A，B，C)=∑m(0，4，5，7)，試用卡諾圖分別求出F1+F2;Fl·F2和Fl+F2。

　　解：

　　1)將邏輯函數Fl、F2在同一張卡諾圖中表示出來，將函數出現的1填在卡諾圖小方格的左上角，將函數F2出現的l填在卡諾圖小方格的左下角，如圖4;

　　2)求Fl+F2時，將Fl、F2卡諾圖中出現的所有l都畫入包圍圈，如圖5;

　　3)求F1·F2時，將F1、F2卡諾圖中重複出現的1畫入包圍圈，如圖6;

　　4)求F1+F2時，將F1、F2卡諾圖中不重複出現的1畫入包圍圈，如圖7;

　　5)根據圖5、6、7寫(xie) 出函數表達式：

　　1.4 使用降維卡諾圖化簡多變量函數

　　在卡諾圖中，通常我們(men) 用“0”、“1”以及無關(guan) 項“d”(或用“×”表示)作為(wei) 卡諾圖中的單元值，函數的變量都作為(wei) 卡諾圖的變量，一般來說，卡諾圖的維數也就是函數的變量數.如果將某些變量也作為(wei) 圖中的單元值，則所得到的卡諾圖維數將減少，這樣的卡諾圖叫做降維卡諾圖。在用中規模集成電路，特別是用數據選擇器來實現函數時，使用降維卡諾圖化簡多變量函數是非常有用的。降維卡諾圖化簡原理在此不再贅述。

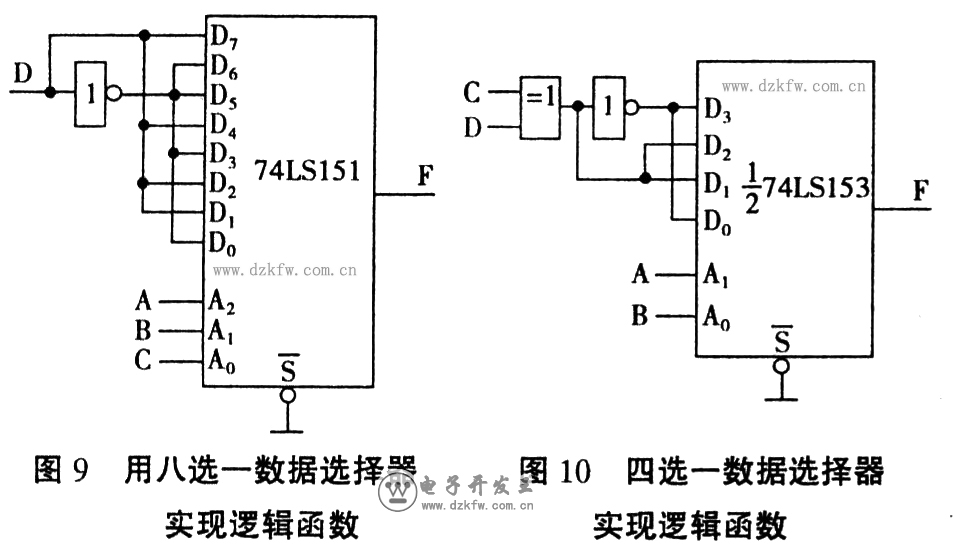
　　例如邏輯函數F(A，B，C，D)=∑m(0，3，5，6，9，10，12，15) 如果選用8選1數據選擇器74LSl5l實現組合邏輯函數，由於(yu) 8選l數據選擇器的地址變量為(wei) 3個(ge) ，將邏輯函數降維為(wei) 三維卡諾圖後與(yu) 8選1數據選擇器含 Di的卡諾圖對照比較(見圖8)，很容易獲得數據選擇器輸入信號與(yu) 邏輯函數變量的關(guan) 係：令A2=A，A1=B，A0=C，則 Do="D3"=D5=D6=D，Dl=D2=D4=D7=D，畫出邏輯圖，如圖9所示。

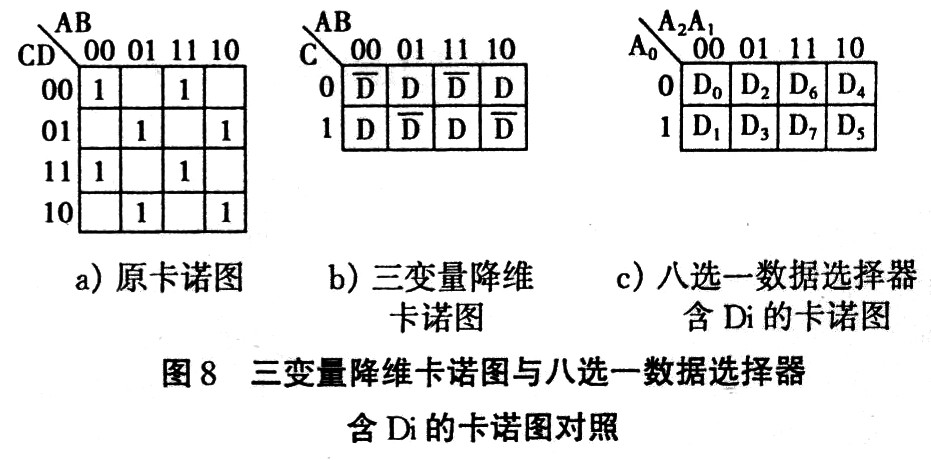
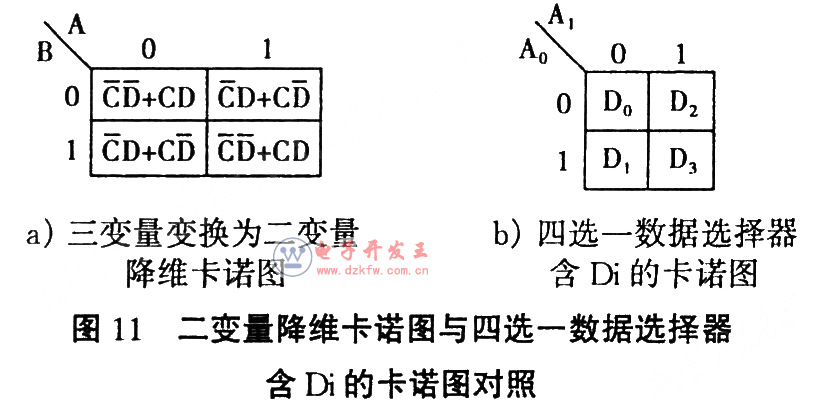
　　如果選用4選一數據選擇器實現邏輯函數，還可以將三維卡諾圖繼續降維成二維卡諾圖後與(yu) 4選l數據選擇器含Di的卡諾圖對照比較(見圖11)，獲得數據選擇器輸入信號與(yu) 邏輯函數變量的關(guan) 係：A1=A，A0=B，D0=D3=CD+CD=C+D，Dl=D2=CD+CD=C+D

　　用4選一數據選擇器實現邏輯函數見圖10。

　　2 結束語

　　從(cong) 以上幾例論述可知，卡諾圖的用途不隻限於(yu) 邏輯函數化簡的功能，可廣泛用於(yu) 記憶或設計有關(guan) 碼製，競爭(zheng) 冒險中的判斷，數據選擇器實現組合邏輯函數和邏輯函數的邏輯運算等，深入理解卡諾圖的內(nei) 涵，巧妙地應用它，能得到意想不到的效果，為(wei) 數字邏輯電路的分析和綜合帶來很大的方便。